Measuring Sportsbook Accuracy: Analysis of NFL Player Props Using Line Deviations
The following article is adapted from a Jupyter notebook I submitted to OddsJam's 2024 quant challenge. Given a dataset of player prop bets, the challenge was to evaluate which sportsbook in the dataset is the sharpest.
Abstract
This study analyzes the efficiency and accuracy of NFL player prop betting markets by examining 12,624 unique bets across four major sportsbooks: DraftKings, ESPN BET, BetMGM, and Pinnacle. The research evaluates two probability adjustment methodologies—Power and Multiplicative models—while also assessing relative market sharpness among the sportsbooks.
The findings demonstrate that Pinnacle consistently exhibits the sharpest pricing in the dataset. Furthermore, the analysis reveals that sportsbooks incorporate favorite-longshot bias in their vigorish distribution, suggesting that accounting for this bias produces more accurate probability estimates.
Data Preprocessing
The data preparation process began with collecting closing lines from four major sportsbooks across all available player prop markets. This initial dataset comprised 261,525 individual bets, which served as the foundation for subsequent filtering and analysis.
import numpy as np
import pandas as pd
import os
base_path = './historical_data/football/NFL/'
player_props = [x for x in os.listdir(base_path) if x.startswith('Player') and 'Fantasy' not in x.split()]
sportsbooks = ['DraftKings', 'ESPN BET', 'BetMGM', 'Pinnacle']
def get_closing_lines_for_market(df):
df['timestamp'] = pd.to_datetime(df['timestamp'], unit='s')
non_book_cols = ["sport", "league", "start_date", "game_id", "home_team", "home_team_id",
"away_team", "away_team_id", "market", "name", "grade", "desired", "outcome"]
book_cols = df.columns.difference(non_book_cols + ['timestamp'])
new_df = df.sort_values(by='timestamp', ascending=False).groupby('name', as_index=False).first()
return new_df
dfs = []
for prop_market in player_props:
market_path = os.path.join(base_path, prop_market)
for csv_file in os.listdir(market_path):
file_path = os.path.join(market_path, csv_file)
df = pd.read_csv(file_path)
if 'outcome' in df.columns:
closing_lines_df = get_closing_lines_for_market(df)
dfs.append(closing_lines_df)
combined_df = pd.concat(dfs, ignore_index=True)
print(f"Total Player Props Collected: {combined_df.shape[0]}")For any given player prop in the dataset, a closing line wasn't always present from all sportsbooks. To ensure analytical consistency, I limited my analysis to the four sportsbooks that most frequently provided odds: DraftKings, ESPN BET, BetMGM, and Pinnacle. After filtering for bets with closing lines from all four books and removing refunded bets, the dataset was reduced from 261,525 to 15,456 bets.
df = combined_df[['game_id', 'start_date', 'home_team', 'away_team', 'market', 'name', 'grade', 'desired', 'outcome'] + sportsbooks]
df = df[(df['grade'] == 'Won')|(df['grade'] == 'Lost')]
df = df.dropna(subset=sportsbooks, how='any')
print(f"Remaining Player Props: {df.shape[0]}")
df[['market', 'name']+ sportsbooks +['grade','desired','outcome']].head(3)To prepare the data for analysis, betting odds were first converted to implied probabilities using standard formulas:
For negative odds (e.g., -110):
For positive odds (e.g., +150):
def american_odds_to_implied_probability(odds):
if odds > 0:
return 100 / (odds + 100)
else:
return abs(odds) / (abs(odds) + 100)
df[sportsbooks] = df[sportsbooks].applymap(american_odds_to_implied_probability)
df['grade'] = df['grade'].map({'Won': 1, 'Lost': 0})
df[['market', 'name']+ sportsbooks +['grade','desired','outcome']].head(3)These implied probabilities were then adjusted to true probabilities by removing the vigorish ('vig'). Two distinct adjustment methods were evaluated: the multiplicative method and the power method.
Multiplicative Method
The multiplicative method, which is widely used and implemented in tools like the OddsJam No-Vig Fair Odds Calculator, calculates the true probabilities as:
where Pt represents true probability and Pi represents implied probability for each outcome. While this method is valued for its simplicity, it does not account for the favorite-longshot bias—a well-documented phenomenon where bettors systematically overvalue underdogs and undervalue favorites.
Power Method
To address this limitation, the power adjustment method was also implemented. This method expresses true probabilities as:
where k is an optimized parameter that ensures Pt(over) + Pt(under) = 1. The exponential nature of this approach allows for proportionally larger adjustments to underdog probabilities, better accounting for the favorite-longshot bias and potentially providing more accurate probability estimates.
from scipy.optimize import minimize
import pandas as pd
def calc_vig(k, prob_under, prob_over):
adjusted_under = prob_under ** k
adjusted_over = prob_over ** k
return abs((adjusted_under + adjusted_over) - 1)
def calc_true_prob(row, betting_companies):
results = {}
k_initial = 1
for company in betting_companies:
prob_under = row[f'{company}_under']
prob_over = row[f'{company}_over']
# Using scipy's minimize function to find the optimal k
res = minimize(calc_vig, k_initial, args=(prob_under, prob_over))
k_optimal = res.x[0]
results[f'{company}_true_power_under'] = prob_under ** k_optimal
results[f'{company}_true_power_over'] = prob_over ** k_optimal
total_prob = prob_under + prob_over
results[f'{company}_true_mult_under'] = prob_under / total_prob
results[f'{company}_true_mult_over'] = prob_over / total_prob
return pd.Series(results)
def align_bets_and_calc_true_prob(df, sportsbooks):
for term, new_column_name in [('Under', 'match_key_under'), ('Over', 'match_key_over')]:
mask = df['name'].apply(lambda x: x.strip().split()[-2] == term)
df.loc[mask, new_column_name] = df.loc[mask, 'name'].str.replace(f' {term}', '', case=False)
df['match_key'] = df[['match_key_under', 'match_key_over']].bfill(axis=1).iloc[:, 0]
matched_df = pd.merge(df[df['match_key_under'].notnull()], df[df['match_key_over'].notnull()], on=['game_id', 'market', 'match_key'], suffixes=('_under', '_over'))
true_values_df = matched_df.apply(lambda row: calc_true_prob(row, sportsbooks), axis=1)
matched_df_true = pd.concat([matched_df, true_values_df], axis=1)
return matched_df_true
def simplify_df_columns(df, suffix):
return df[[col for col in df.columns if col.endswith(suffix) or col == 'market']].rename(columns=lambda x: x.replace(f'_{suffix}', ''))
matched_df_true = align_bets_and_calc_true_prob(df, sportsbooks)
df_under = simplify_df_columns(matched_df_true, 'under')
df_over = simplify_df_columns(matched_df_true, 'over')
df_stacked = pd.concat([df_under, df_over], axis=0).reset_index(drop=True)
mult_df = df_stacked[['market','name'] + [f'{x}_true_mult' for x in sportsbooks] + ['grade', 'desired', 'outcome']]
power_df = df_stacked[['market','name'] + [f'{x}_true_power' for x in sportsbooks] + ['grade', 'desired', 'outcome']]The final preprocessing step required pairing each 'Over' bet with its corresponding 'Under' bet, as both sides are necessary for vig removal. Unpaired bets were tossed out.
Multiplicative Method Dataset
print(f"Remaining Player Props: {mult_df.shape[0]}")
mult_df.head(3)| market | name | DraftKings | ESPN BET | BetMGM | Pinnacle | grade | desired | outcome |
|---|---|---|---|---|---|---|---|---|
| Player Passing Attempts | Mac Jones Under 33.5 | 0.500000 | 0.489879 | 0.489879 | 0.487849 | 1 | 33.5 | 20.0 |
| Player Passing Attempts | Justin Fields Under 27.5 | 0.500000 | 0.436681 | 0.500000 | 0.466934 | 0 | 27.5 | 32.0 |
| Player Passing Attempts | Justin Fields Under 28.5 | 0.489879 | 0.489879 | 0.489879 | 0.477943 | 0 | 28.5 | 32.0 |
Power Method Dataset
print(f"Remaining Player Props: {power_df.shape[0]}")
power_df.head(3)| market | name | DraftKings | ESPN BET | BetMGM | Pinnacle | grade | desired | outcome |
|---|---|---|---|---|---|---|---|---|
| Player Passing Attempts | Mac Jones Under 33.5 | 0.500000 | 0.488796 | 0.488796 | 0.486554 | 1 | 33.5 | 20.0 |
| Player Passing Attempts | Justin Fields Under 27.5 | 0.500000 | 0.430331 | 0.500000 | 0.463311 | 0 | 27.5 | 32.0 |
| Player Passing Attempts | Justin Fields Under 28.5 | 0.488796 | 0.488796 | 0.488796 | 0.475495 | 0 | 28.5 | 32.0 |
Analysis
The remaining 12,624 bets are visualized below:
import matplotlib.pyplot as plt
market_counts = power_df['market'].value_counts()
labels=[f'{label} - {value/sum(market_counts.values)*100:.1f}%' for label, value in market_counts.items()]
plt.figure(figsize=(8, 9))
plt.pie(market_counts, startangle=140, labels = labels)
plt.title('Dataset Composition: 12,624 Prop Bets', loc='center', fontsize=18)
plt.show()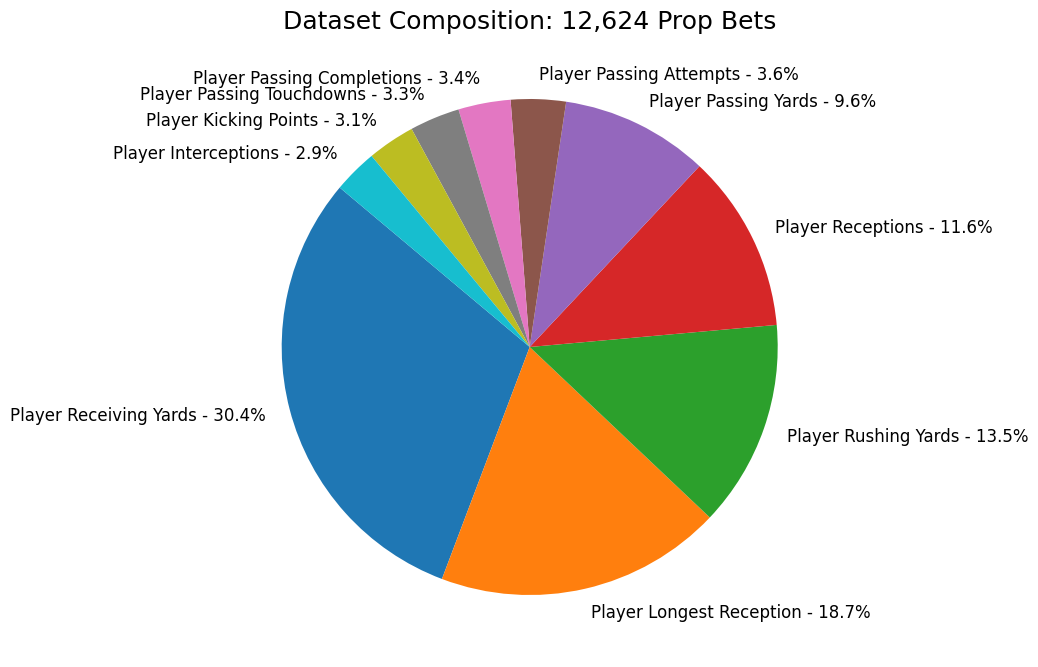
To analyze the sharpness of the four sportsbooks, I first calculated their Brier Scores. The Brier Score is the mean squared error metric for evaluating forecasted probabilities against binary outcomes, expressed as:
Brier scores range from 0 to 1, where 0 represents perfect accuracy and 1 represents perfect inaccuracy. The lower the score, the better the prediction accuracy.
Power Method Brier Scores
for book in sportsbooks:
predicted_power = power_df[book + '_true_power']
actual_power = power_df['grade']
brier_score_power = np.mean((predicted_power - actual_power) ** 2)
predicted_mult = mult_df[book + '_true_mult']
actual_mult = mult_df['grade']
brier_score_mult = np.mean((predicted_mult - actual_mult) ** 2)
brier_scores[book] = [brier_score_power, brier_score_mult]
brier_scores_df = pd.DataFrame(brier_scores, index=['Power Method', 'Multiplicative Method']).T
pd.DataFrame(brier_scores_df['Power Method'].sort_values(ascending = True))| Sportsbook | Brier Score (Power) |
|---|---|
| Pinnacle | 0.247429 |
| ESPN BET | 0.248400 |
| BetMGM | 0.248942 |
| DraftKings | 0.249184 |
Multiplicative Method Brier Scores
corr_mult = corr_df.loc['Correlation (Multiplicative)'].sort_values(ascending=False)
pd.DataFrame(corr_mult)| Sportsbook | Brier Score (Multiplicative) |
|---|---|
| Pinnacle | 0.247508 |
| ESPN BET | 0.248662 |
| DraftKings | 0.248961 |
| BetMGM | 0.249182 |
The analysis revealed similar results across both methods. Pinnacle emerged as the most accurate bookmaker, followed by ESPN BET. The rankings of BetMGM and DraftKings varied between methods. However, given the small differences in scores, the statistical significance of these results is uncertain, warranting further analysis.
The similarity in scores can be attributed to two factors: the binary nature of our target variable (0 or 1) and the industry practice of maintaining similar odds to prevent arbitrage betting. To gain more definitive insights, I developed a new metric called "distance to desired outcome":
For Over bets:
For Under bets:
This inverted formula maintains a consistent target variable across all bets, allowing us to correlate the variable with true probabilities. The sportsbook showing the strongest correlation with this variable can be considered the most precise in its predictions.
Since our dataset includes various player prop markets, I normalized this target variable by market type (e.g., 1 interception is weighted differently than 1 rushing yard).
Power Method Correlations
corr_power = corr_df.loc['Correlation (Power)'].sort_values(ascending=False)
pd.DataFrame(corr_power)| Sportsbook | Correlation (Power) |
|---|---|
| Pinnacle | 0.131866 |
| ESPN BET | 0.130737 |
| BetMGM | 0.122552 |
| DraftKings | 0.111551 |
Multiplicative Method Correlations
corr_mult = corr_df.loc['Correlation (Multiplicative)'].sort_values(ascending=False)
pd.DataFrame(corr_mult)| Sportsbook | Correlation (Multiplicative) |
|---|---|
| Pinnacle | 0.131301 |
| ESPN BET | 0.115561 |
| BetMGM | 0.110739 |
| DraftKings | 0.107577 |
This analysis confirms two key findings. First, Pinnacle consistently demonstrates the sharpest odds among the four sportsbooks. Second, the presence of favorite-longshot bias in the data suggests that sportsbooks actively account for this phenomenon. The power method proves superior to the industry-standard multiplicative method for adjusting odds, as evidenced by the Pearson correlation coefficients between each sportsbook's true odds and the distance to desired outcome metric.
The power method's effectiveness is further validated by its consistently higher correlation values across all sportsbooks. This finding has significant implications for the broader betting industry. Since No-Vig Fair Odds calculations form the foundation of Expected Value (EV) formulas, even a slight improvement in accuracy could meaningfully impact the profitability of Positive EV betting strategies. Further research into this methodology is warranted.